[Algorithm/Java] 알고리즘 자바 미로탐색 DFS (코딩테스트, DFS, BFS, 미로찾기)

---

1. 문제 설명

• 설명
  7*7 격자판 미로를 탈출하는 경로의 가지수를 출력하는 프로그램을 작성하세요.
  출발점은 격자의 (1, 1) 좌표이고, 탈출 도착점은 (7, 7)좌표이다. 격자판의 1은 벽이고, 0은 통로이다.
  격자판의 움직임은 상하좌우로만 움직인다. 미로가 다음과 같다면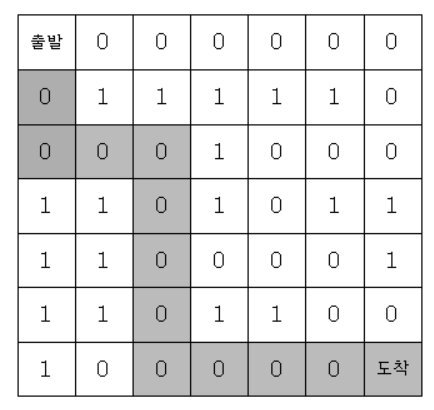
  
  위의 지도에서 출발점에서 도착점까지 갈 수 있는 방법의 수는 8가지이다.
• 입력
  7*7 격자판의 정보가 주어집니다.
• 출력
  첫 번째 줄에 경로의 가지수를 출력한다.

 

 

2. 문제 코드 및 풀이 설명

import java.util.Scanner;

public class Maze {
  // 미로를 찾는 방향을 설정한 배열
  static int[] dx = {-1, 0, 1, 0};
  static int[] dy = {0, 1, 0, -1};
  // 미로가 입력될 배열
  static int[][] board;
  static int answer = 0;

  public static void main(String[] args) {
    Maze T = new Maze();
    Scanner kb = new Scanner(System.in);

    board = new int[8][8];
    for (int i = 1; i <= 7; i++) {
      for (int j = 1; j <= 7; j++) {
        board[i][j] = kb.nextInt();
      }
    }
    board[1][1] = 1; // 시작점을 1로
    T.DFS(1, 1); // (1,1)부터 시작
    System.out.println(answer);
  }

  // 미로찾기 알고리즘
  // 현재 지점에서 좌, 상, 우, 하 방향으로 갈 수 있는 지를 체크
  // 갈 수 있다면 현재 위치를 1로 바꿔주고 다음 위치로 이동
  // 이동해서 재귀함수를 호출 후 재귀함수가 끝나면 다시 이전 위치를 0으로 바꿔줌
  public void DFS(int x, int y) {
    if (x == 7 && y == 7) answer++; // 마지막 지점에 도착한 경우 경우의 수 추가
    else {
      for (int i = 0; i < 4; i++) { // 좌, 상, 우, 하 방향 체크
        // 예) 좌 방향이라면 dx[0] = -1, dy[0] = 0을 저장해 놓았으니 현재 위치에서 더해주면 왼쪽으로 한 칸이동
        int nx = x + dx[i];
        int ny = y + dy[i];
        // 만약 이동하려는 방향이 0이 들어있다면, 곧 아직 지나오지 않은 경로라면
        if (nx >= 1 && nx <= 7 && ny >= 1 && ny <= 7 && board[nx][ny] == 0) {
          board[nx][ny] = 1; // 경로체크
          DFS(nx, ny); // 재귀함수 호출
          board[nx][ny] = 0; // 호출 후 다시 경로를 원래 상태로로
        }
      }
    }
  }
}

 

3. 출력 예시

입력
0 0 0 0 0 0 0
0 1 1 1 1 1 0
0 0 0 1 0 0 0
1 1 0 1 0 1 1
1 1 0 0 0 0 1
1 1 0 1 1 0 0
1 0 0 0 0 0 0

출력
8

 

 

 

 

---

위의 내용은 인프런에서 수강할 수 있는 김태원님의 자바 알고리즘 문제풀이 강의를 바탕으로 공부한 내용을 정리한 내용입니다!

https://inf.run/iAi6

자바(Java) 알고리즘 문제풀이 : 코딩테스트 대비 - 인프런 | 강의